Scattering from a Gaussian Chain

3.2 Scattering from a Gaussian Chain

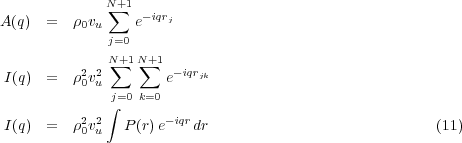
The scattering from an independent polymer chain following Gaussian statistics was solved by Debye [7]. The derivation is based on an evaluation of the intensity as a double sum resulting from the square of the expression for the amplitude of the scattered wave.

N+1 A (q) = ρ v ∑ e-iqrj 0 u j=0 N+1N+1 I(q) = ρ2v2 ∑ ∑ e-iqrjk 0 u j=0 k=0 ∫ I(q) = ρ20v2u P(r)e-iqrdr (11)

where v_u is the volume of a monomer, the polymer is made up of N + 1 such monomers, and P(r) represents the number of monomer pairs that are separated by r. It is via this last term that the Gaussian distribution enters, as P(r) is a function of the distribution in the square brackets below

[ ] N∑ ( 3 )3∕2 ( 3r2 ) P(r) = 2 (N + 1- K ) 2πKl2- exp -2Kl2- K=0

where there are (N + 1 - K) pairs of monomers separated by K bonds, and the bond length is l.

The solution is

I(q) = ρ2ov2uD(x) 2(e-x + x - 1) 2 2 D(x) = -----x2------; x = q R g (12)

At small q, it can be approximated as

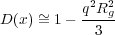
2 2 D (x) ~= 1- q-R-g 3

3.2.1 Length Scales

The Gaussian distribution contains no inherent length scale - Gaussian (ideal) chains obey the statistics down to and out to aphysical dimensions. In reality, we understand that there is a length scale below which the polymer chain appears locally stiff due to the persistence of bond orientation for a finite monomer sequence. We should thus expect a crossover from rod-like scattering to Gaussian like scattering at a particular scattering vector, corresponding to the persistence length. This is in fact the case. At small q, the scattering is shape independent and scales as exp(-q²). At slightly larger q, we observe the 1∕q² dependence of the Debye formulation, and at even larger q, a q^-1 dependence of intensity, characteristic of rod-like scattering. This is well illustrated on a Kratky plot of I(q).q² vs q [1].

3.2.2 Guinier’s Law

Guinier’s law results from an expansion of the exponential dependence of the scattering intensity in Equation 7

∫ A(q) = ρ(r)e-iqrdr ∫ ∫ 1-∫ 2 A(q) = ρ(r)dr - i qrρ(r)dr - 2! (qr) ρ(r) dr+ ... (13)

Given that (qr)² = (q_xx + q_yy + q_zz)², the expression ultimately yields

( ) I(q) = ρ20v2 1 - 1q2R2g +... ( 3 ) 2 2 q2R2g I(q) ~= ρ0v exp ---3-- (14)

A plot of lnI(q) vs. q² has a slope of -R_g²∕3. Guinier’s law is applicable in the regime where qR_g ≤ 1.3 and can only be applied in dilute solution scattering where there are no positional correlations between individual polymer chains. The radius of gyration is shape independent. An extrapolation of the scattered intensity in absolute units back to q = 0 makes it possible to determine the value of (ρ₀v)² if the concentration of particles is known, since I(q) is the scattered intensity per particle. Knowledge of the volume per particle and the radius of gyration gives some information about the shape of the particle (polymer chain). Additionally, molecular weight can be determined, as will be discussed in a later section.

[next] [prev] [prev-tail] [front] [up]