Scattering from a Collection of Atoms

2.2 Scattering from a Collection of Atoms

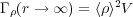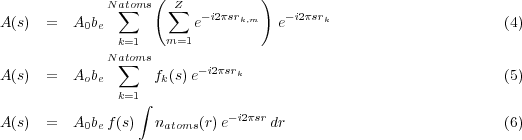
If we now have a collection of atoms, we can describe the location of all electrons in the system with respect to the atom to which they belong as r_j = r_k + r_k,m where k denotes the atom number, and r_k,m denotes the m^th electron of the k-atom. From Equation 2 we can write the scattered amplitude as

Natoms( Z ) A(s) = A b ∑ ∑ e-i2πsrk,m e- i2πsrk (4) 0 e k=1 m=1 Natoms A(s) = A b ∑ f (s)e- i2πsrk (5) o e k=1 k ∫ A(s) = A0bef(s) natoms (r)e-i2πsr dr (6)

Here, we see that the scattered amplitude has a component that depends on the scattered amplitude from one atom, and a component that depends on the distribution of atoms. So called contributions from form and structure factors are ubiquitous in the treatment of scattering from discrete objects such as polymer coils or colloidal particles in solution.

2.2.1 Scattering and the Autocorrelation Function

We can rewrite Equation 2 as

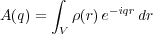∫ A(q) = ρ(r)e-iqrdr V

(7)

where ρ(r) = b_e n(r) is the scattering length density distribution. This says that the scattered amplitude is related to the Fourier transform of ρ(r). Likewise, it can be shown [1] that the intensity, I(q) = |A(q)|²is given by

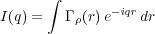
∫ I(q) = Γ ρ(r)e-iqrdr

where

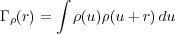
∫ Γ ρ(r) = ρ(u )ρ(u +r)du

is the autocorrelation function of the scattering length density distribution. So the scattered intensity is related to the Fourier transform of this autocorrelation function where

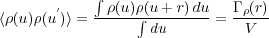
∫ ′ --ρ(u)ρ(u-+-r)du Γ ρ(r) ⟨ρ(u)ρ(u)⟩ = ∫ du = V

At r = 0

Γ ρ(0) = ⟨ρ2⟩V

and at r →∞

Γ (r → ∞ ) = ⟨ρ⟩2V ρ

[next] [prev] [prev-tail] [front] [up]