[next] [prev] [prev-tail] [tail] [up]

3.1 Spheres, Rods, Disks

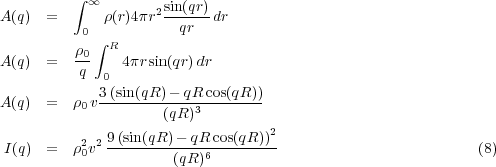
Using Equation 7, we can determine the scattered intensity for a solid sphere of radius R with a uniform density ρ0 for r ≤ R.

∫ ∞ 2 sin(qr)- A (q) = 0 ρ(r)4πr qr dr ρ0 ∫ R A (q) = -- 4πr sin(qr)dr q 0 A (q) = ρ0v 3(sin(qR)--qR-cos(qR-))- (qR )3 2 2 9-(sin(qR-)--qR-cos(qR))2 I(q) = ρ0v (qR )6 (8)

Zeros of the function occur where qR = tan(qR) as shown in Figure 2

PIC

Figure 2: Scattering from an individual solid spherical particle of radius R

For a rod, the expression is given by

[ ] I(q) = ρ20v2-2- Si(qL)- 1---cos(qL) (9) qL qL

where

∫ xsin(u) Si(x) ≡ --u--du 0

For a thin circular disk, the scattered intensity is given in Equation 10 where J1 is the first order Bessel function.

[ ] I(q) = ρ20v2--2-- 1- J1(2qR) (10) q2R2 qR

PIC

Figure 3: Scattering from individual particles of different shape, as a function of the dimensionless product qRg.
3.1.1 Scaling at high q

At high q, the intensity scales as I(q) ~ q-α where α = 4 for spheres, 2 for thin disks and 1 for rods. At small q, the intensities are independent of the shape of the particles, if plotted as a function of qRg, which provides the basis for the Guinier law.

[next] [prev] [prev-tail] [front] [up]