2 Ideal Chain Models

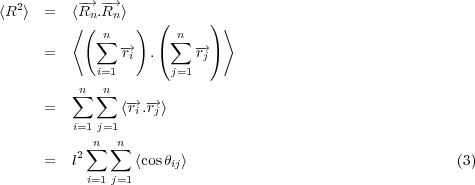
Here we consider ideal chains, that like ideal gases, feature no net interaction (repulsive or attractive) among the n monomers, each with bond length l. We start with a description of the end to end distance of the chain. Given the random nature of displacements of monomers with respect to each other, the mean end-end distance, < R >= 0. The first non-trivial moment of the distribution of end-end distances is the second moment, so we look at the mean squared end-end distance, < R² >, defined in Equation 3.