Freely Rotating Chain

2.2 Freely Rotating Chain

All bond lengths and angles are the same
We have to determine the correlation among the bond vectors of the chain, the distance over which the direction of a particular vector may persist.

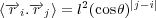
Correlations are transferred along the direction of bond vectors.

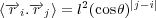⟨-→r i.-→r j⟩ = l2(cosθ)|j-i|

(6)

n∑ (i∑-1 n∑-i ) ⟨R2 ⟩ = nl2 + l2 coskθ + coskθ i=1 k=1 k=1 (cosθ)|j-i| = exp(|j - i|ln(cosθ)) ( |j - i|) = exp - ----- (7) sp

where s_p is a persistence number, s_p = -1∕ln(cosθ). This leads to the final result that

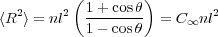( ) ⟨R2 ⟩ = nl2 1+-cosθ- = C nl2 1- cosθ ∞

(8)

For saturated carbon chains, θ = 68^∘ so C_∞≈ 2.

2.2.1 Worm-Like Chain Model

For very stiff chains, the worm-like chain model is applied. Here, the bond angle θ is small and we make approximations for cosθ and ln(cosθ) as used in the derivation for the freely rotating chain.

sp ~= 2∕θ2 C ~= 4∕θ2 ∞ 4 b ~= l-2 = 2lp 2 θ 2 ⟨R ⟩ = 2lpRmax - 2lp(1- exp(- Rmax ∕lp)) (9)

: In the limit where the chain is very long compared to its persistence length, R_max ≫ l_p. < R² > 2l_pR_max = bR_max. This is the ideal chain limit.
: In the limit where the chain is short compared to its persistence length, R_max ≪ l_p. < R² > R_max². This is the rod-like limit

Figure 3:

Mean square end to end distance in the WLC model as a function of persistence length, showing the cross over from ideal to rigid rod behavior

[next] [prev] [prev-tail] [front] [up]