[next] [prev] [prev-tail] [tail] [up]

1.3 Intrinsic Viscosity Determination

We can either use the Huggins equation, which is derived from a virial expansion of the specific viscosity in powers of the intrinsic viscosity, or the Kraemer equation, which results from an expansion of the inherent viscosity, to determine the intrinsic viscosity.

1.3.1 Huggins Equation

The specific viscosity is related to the intrinsic viscosity by a power series of the form

2 3 ηsp = k0[η]c+ k1[η] c2 + k2[η] c3 + ...

where k0,k1,k2... are dimensionless constants, and k0 = 1.

Dividing by concentration, and truncating to only the second term, we form the Huggins equation as

ηsp∕c = [η]+ kH [η]2c
(6)

The constant kH is termed the Huggins constant and has values ranging from 0.3 in good solvents to 0.5 in poor solvents. It contains information about hydrodynamic and thermodynamic interactions between coils in solution. A plot of the reduced viscosity, extrapolated to zero concentration yields the intrinsic viscosity.

1.3.2 Kraemer Equation

We may construct another expansion based on the relative viscosity, in dilute solutions where the specific viscosity is much less than 1.

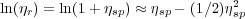
ln(ηr) = ln(1+ ηsp) ≈ ηsp - (1∕2)η2sp

Using the expression for the specific viscosity in the Huggins equation above, Eq. 6, provides Equation 7, the Kraemer equation.

2 ln(ηr) = [η]c+ (kH - 1∕2) [η] c2 ln(ηr)∕c = [η]c+ kK [η]2c (7)

A plot of the inherent viscosity, extrapolated to zero concentration, yields the intrinsic viscosity. Viscometry yield a viscosity average molecular weight, 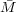¯ Mν where

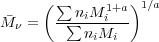
(∑ )1∕a M¯ = --∑niMi1+a- ν niMi

where ni is the number density of chains of molar mass Mi.

[next] [prev] [prev-tail] [front] [up]