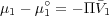
Osmometry provides absolute measurements of molecular weight. It relies on Flory-Huggins lattice theory for a connection between the chemical potential of a solution and the polymer-solvent interaction along with the size of the polymer.
From thermodynamics, we know that the difference between the chemical potential of the solvent in the solution and that in the pure state is given as
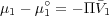
where the molar volume of the solvent, 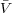 1 is presumed to be independent of pressure. From F-H
theory,
1 is presumed to be independent of pressure. From F-H
theory,
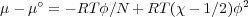
where N is the degree of polymerization, or the number of lattice sites occupied by the polymer and χ is related to the Gibbs free energy difference for the formation of a solvent-monomer contact, Δg12 = g12 - (1∕2)(g11 + g22) on a lattice of coordination z
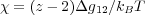
This provides
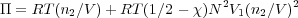
where n1 and n2 are he number of solvent and polymer molecules respectively. The number density of polymer
molecules is related to the mass concentration and molecular weight as n2∕V = (m∕V )(n2∕m) = c∕ n since the
number average molecular weight is given as
n since the
number average molecular weight is given as
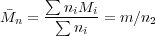
We can now write:
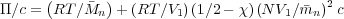
From the lattice theory, N = V 2∕V 1 and so NV 1∕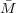 n = V 2∕
n = V 2∕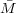 n = 1∕ρ2 so we arrive at Equation
8.
n = 1∕ρ2 so we arrive at Equation
8.
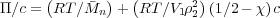 | (8) |
Under theta conditions, χ = 1∕2 and so
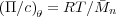
In general, we can evaluate RT∕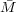 n as the value of the reduced osmotic pressure in the zero concentration limit,
so
n as the value of the reduced osmotic pressure in the zero concentration limit,
so
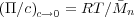
The remaining term yields the second virial coefficient, providing information about the thermodynamics of the system. The theta temperature can be evaluated by plotting the value of the second virial coefficient and finding where it is equal to zero.
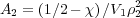 | (9) |