|
|
Ab Initio Laser Theory and Random Lasers:
|
|
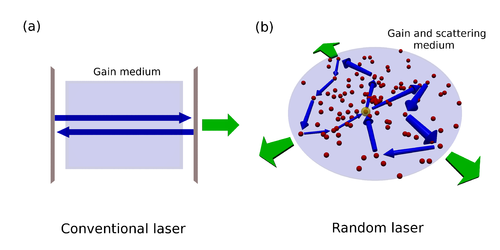
Conventional laser versus a diffusive random laser: (a) A conventional laser cavity has highly-reflecting mirrors which trap light long enough for amplification by the gain medium (light blue) to be efficient. The oscillation frequencies are well-defined and are given by "resonance conditions": light has to make an integer number of oscillations upon a roundtrip ("loop") along the length of the cavity. (b) In a random laser, the trapping of light is not achieved by mirrors, but by multiple scattering between sub-wavelength particles (red dots) in this specific realization. In such a random medium the light emitted by an atom (yellow) can make a roundtrip in an infinite number of loops (two of which are indicated). In the special case of a diffusive random laser, the scattering is so weak that without gain most of the light would escape before returning to its starting point. Due to this strong damping (leakage), the oscillation frequencies of such a system are not well-defined. However, when lasing sets in, a number of well-defined, sharp oscillation frequencies appear (see Figure 3) which bear no straightforward relationship to the strongly damped natural oscillations of the system without gain.
|
Despite the fact that lasers are one of the most important inventions of the 20th century, the theory of lasers which emit at many frequencies (multimode lasing) is surprisingly underdeveloped, even though such lasers are quite common. The reason for the lack of a predictive theory for such lasers is two-fold. First, the fact that the laser cavity is an open system must be taken into account fully (which is technically difficult), and second, when several modes are emitting laser radiation they interact in a complex non-linear manner.
Recently my group has developed the first time-independent theory which handles both of these challenges, and have applied it to a system, the diffusive random laser, which cannot be treated at all by conventional laser theory, due to its extreme openness. As a consequence, for the first time we are able to answer the question: what does the electric field look like inside a diffusive random laser? More generally our theory is part of the answer to the fundamental question: How does a laser work?

|
|
(Suggestion for the Cover of Science): Planar realization of a random laser that is pumped with incoherent light from the top and emits coherent light in random directions. In a random laser, light is confined to a gain medium not by conventional mirrors but by random multiple scattering.
|
|
|
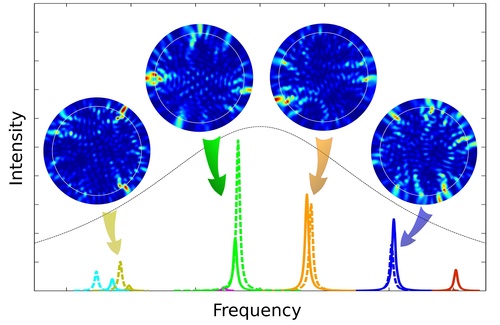
Diffusive random lasers produce coherent laser light at several frequencies (multi-mode lasing). Strong interactions between modes suppress a large number of possible oscillation frequencies of the system, leading to a well-separated frequency spectrum under the gain curve (black dashed curve) as shown above. While the emission intensities of the individual lasing modes are highly susceptible to spatial fluctuations of the pump source, emission frequencies remain relatively stable (solid lines show intensities for uniform pumping and dashed lines for nonuniform pumping). The circular insets display the field distributions of the lasing modes specific to each lasing frequency (white circles mark the boundary of the gain medium).
|
|
|

