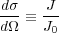
In a light/x-ray scattering experiment, we make some measure of the intensity of the scattered radiation as a function of the angle with respect to the incident beam direction. This intensity is related to the flux of radiation, J, which is proportional to the square of the amplitude of the oscillating field of the radiation, so J = |A|2 = AA* where A* is the complex conjugate of A. For a plane wave, the flux is related to the energy transmitted per unit area per unit time, and is independent of the distance from the source to the area over which the detection is made. For a spherical wave, in order to make the flux independent of the distance, it is measured as the energy transmitted per unit solid angle per unit time.
The sample is irradiated/illuminated with an incident beam of flux J0 and the flux of scattered radiation J is recorded as a function of angle away from the incident direction. The ratio J0∕J has units of area per solid angle, and is formally known as the differential scattering cross section. Strictly speaking, the word intensity (absolute) refers to this ratio, although in the x-ray community, intensity (arbitrary) is used to refer to measurements of the flux J.
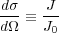
The differential scattering cross section is the probability that a photon impinging on the sample is scattered into a unit solid angle in the given direction [1], that is, the number of particles scattered into a unit solid angle in a given direction per second divided by the flux of the incident beam. The integral of the differential scattering cross section provides the total scattering cross section, σ with dimensions of [L2] or area as
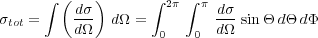
where Θ ≡ 2θ.