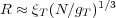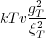
We can conceive of a blob that is associated with the balance between thermal energy and the energetic contribution due to excluded volume interactions. On length scales below ξT, the polymer is ideal whereas above ξT, excluded volume interactions dominate and the system executes a self-avoiding random walk.
The blob is ideal, so ξT2 ≈ gTb2. As above, using a mean field number density of monomers inside the blob, the excluded volume interaction energy is
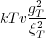
This energy is just balanced by the thermal energy, kT so that the thermal blob size is given by ξT ≈ b4∕v and the number of monomers in a blob as gT ≈ b6∕v2. Comparison to Equation 5 shows that the number of monomers in the thermal blob is related to the chain interaction parameter by
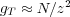
If we now consider the conformation of the chain above the blob length scale, for excluded volume repulsion, the blobs follow a self-avoiding random walk, so

where ν ≈ 3∕5 as provided by the Flory argument. For excluded volume attraction, the blobs condense onto themselves, and form a compact globule. The size of the globule is given assuming a fractal dimension of 3, that is