[next] [prev] [prev-tail] [tail] [up]

2 Flory Theory

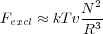
Flory treated the question of equilibrium conformation of real chains using a mean field approach. The equilibrium size is set by a balance between excluded volume which tends to expand the chain size, and a restoring force due to loss of conformational entropy due to swelling. The energetic contribution due to excluded volume is given by the number of excluded volume interactions within a coil and the cost of each exclusion, kT. The number of excluded volume interactions is just the probability of finding a monomer within the excluded volume of another. If we assume a mean density of monomers in the coil, N∕R3, then the number of excluded volume interactions per monomer is vN∕R3 and for N monomers in the coil, the energetic contribution is

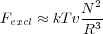F ≈ kTvN-2 excl R3
(3)

The entropic energy due to expansion of the coil is given as

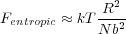
2 Fentropic ≈ kT R-- N b2

The equilibrium coil size is determined as the minimum in the total energy function FT(R) = Fexcl(R) + Fentropic(R). For positive v we have

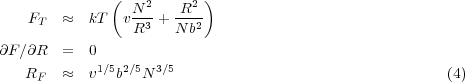
( ) N-2 R2-- FT ≈ kT v R3 + N b2 ∂F∕∂R = 0 1∕52∕5 3∕5 RF ≈ v b N (4)

Comparison of RF with N1∕2b provides a quantity known as the chain interaction parameter, z where

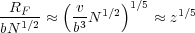-RF-- (-v 1∕2)1∕5 1∕5 bN 1∕2 ≈ b3N ≈ z
(5)

 2.1 Problems with Flory Theory

[next] [prev] [prev-tail] [front] [up]