2 Entropic Free Energy of a Polymer Chain

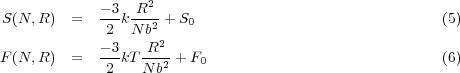
The free energy of an ideal polymer chain is derived from its conformational entropy, described by the probability distribution above. The entropy as a function of the end to end distance R is provided by Boltzmann’s relation S = k lnΩ(R) where Ω(R) is simply the number of ways (conformations) of arranging monomers such that the chain has an end-end distance R. The free energy is given below.

The expressions above in Equation 6 relate the free energy of the polymer chain very simply to a ratio between the end-end distance R and the unperturbed end-end distance, Nb². The force required to perturb the chain dimensions is is just given by

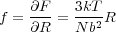(7)

This expression is linear in the displacement R and scales directly with temperature T. i.e. the polymer acts as an entropic spring, and becomes stiffer with increasing temperature. The above expression only holds true for deformations which do not significantly perturb the chain conformation, i.e. which do not make the chain conformation depart from Gaussian statistics. It is valid only in the limit where the deformation is small compared to the contour length of the polymer chain.

For a worm-like polymer chain, an approximate expression is provided by Siggia et al. [?], that fits small and large extensions