[next] [prev] [prev-tail] [tail] [up]

1 Probability Distribution of End-End Distances

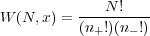
We develop expressions for the probability distribution of end-end distances of a polymer chain. We start from a simple random walk in one dimension, and generalize the result to three dimensions.

In one dimension, the number of ways of arriving a distance x from the origin after N steps of unit size (n+ in the positive direction and n- in the negative) is given by a combinatorial expression.

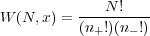---N-!--- W (N,x) = (n+!)(n- !)
(1)

where x = n+ - n-, N = n+ + n- and so n+ = (N + x)∕2, and n- = (N - x)∕2. The probability of this occurrence is just the number of ways of realizing the occurrence divided by the total number of possible trajectories.

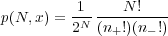1-----N-!--- p(N,x) = 2N (n+!)(n- !)
(2)

We consider the natural logarithm of the above probability. Using Stirling’s approximation, N!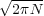~=√ ---- 2πN(N∕e)N, and assuming that x ≪ N we arrive at the probability distribution function, which is the probability p(N,x)dx that the trajectory of the random walk is terminated within an interval dx from x.

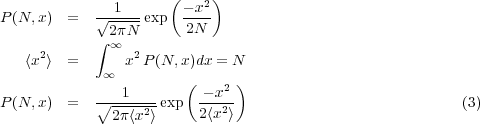
( 2) P (N, x) = √-1---exp - x- ∫ 2πN 2N 2 ∞ 2 ⟨x ⟩ = ∞ x P(N, x)dx = N 1 ( - x2 ) P (N, x) = ∘-----2-exp ---2- (3) 2π⟨x ⟩ 2⟨x ⟩

In three dimensions, the probability P(N,R) is just the product of P(N,Rx)P(N,Ry)P(N,Rz)dxdy dz and since < R2 >= Nb2,

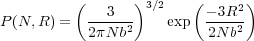( )3∕2 ( 2) P (N,R ) = --3-2- exp --3R2 2πN b 2N b
(4)

so the probability of finding the chain end (terminus of an ideal random walk) in a spherical shell between R and R + dR is P(N,R)4πR2 dR.

[next] [prev] [prev-tail] [front] [up]