
Instead of the end-end distance, the radius of gyration of the macromolecule, Rg is more meaningful intuitively as it gives a sense of the size of the polymer coil. It is also the quantity that is experimentally accessed.
The square radius of gyration is the average squared distance of any point in the object (polymer coil) from it’s center of mass. This definition, along with the final expression for the calculation of the ensemble average of the quantity is provided in Equation 13.
|
The radius of gyration of an equivalent freely jointed chain is given by < Rg2 = Nb2∕6 =< R2 > ∕6. That is, the
radius of gyration is smaller than the root mean square end-end distance by a factor of 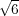 . It is instructive to
remember that the radius of gyration of a solid sphere is not equivalent to its physical radius. For a sphere,
Rg2 = 3R2∕5. The radius of gyration for some common polymer architectures and solid objects is provided in Table
1.
. It is instructive to
remember that the radius of gyration of a solid sphere is not equivalent to its physical radius. For a sphere,
Rg2 = 3R2∕5. The radius of gyration for some common polymer architectures and solid objects is provided in Table
1.