Rheology and microfluidic flows of complex fluids
Kinetic arrest and aging in complex fluids
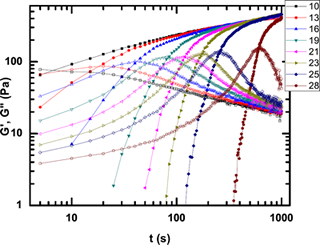
Many disordered complex fluids are inherently out of equilibrium and display glassy dynamics - a slow evolution of their dynamics over time. However, many features of the canonical glass transition as encountered in polymer and molecular glasses are not conserved. This is still not completely understood and in particular little is known about the connection between the mechanical or flow history, as a determinant of the initial state of the system, and the subsequent aging dynamics. The changes in the energy landscape during physical aging can be understood from the frequency and strain dependence of the shear modulus but the non-stationary nature of these systems frustrates investigation of their instantaneous underlying properties. We use bulk rheology to study these phenomena in a variety of systems (particulate suspensions). Stress jump experiments are performed to investigate the role of flow history on aging. Extensive time-dependent studies are used to systematically reconstruct the frequency and strain dependence of the shear modulus as a function of age for colloidal glasses undergoing structural arrest and subsequent aging. We have uncovered a connection between the aging behavior and the rate of flow cessation that is additionally reflected in the dynamics of residual stress relaxation. Strikingly, the frequency dependence at fixed system age can be rescaled onto a master curve, implying a simple connection between the aging of the system and the change in the frequency dependent modulus. Using parallel superposition rheology, our studies examine key differences in the dynamics of structural arrest in repulsive glasses and attractive gels. Repulsive glasses are shown to arrest with the display of a distinctive peak in the loss modulus, with a significant delay and narrowing of the peak induced by shear stresses applied during aging. Conversely, attractive systems display no such signature and instead evolve with a comparatively flat loss modulus during arrest. We speculate that the difference originates due the ability of repulsive systems to form particle cages whereas attractive systems form physically-connected fractal network-like structures.
Shear thickening and structuring in fumed colloidal suspensions
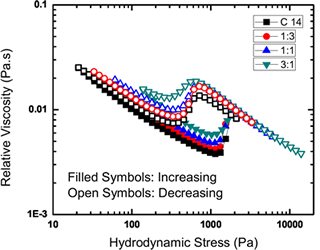
Shear thickening in colloidal dispersions has been described both experimentally and numerically via Stokesian dynamics in concentrated non-flocculating systems with hard sphere or repulsive interactions. It arises from enhanced viscous dissipation due to the forcing of particles into close contact in shear-induced hydroclusters. By contrast, shear thickening in attractively interacting, gel-forming systems is largely unknown and not predicted to occur. Surprisingly, we find that dilute dispersions of attractively interacting fumed colloidal particles (e.g. carbon black) in Newtonian liquids exhibit modest shear thickening behavior under high shear. The transition to shear thickening flow is controlled by a critical stress which determines the onset of shear induced cluster breakup as opposed to hydrocluster formation. The highly structured nature of the fumed particulates is at the origin of this peculiar display. The elastic modulus of shear thickened gels exhibits a power-law dependence on the pre-shear stress, in agreement with simple scaling arguments. Subsequent deformation of shear thickened dispersions results in a dramatic display of transient vorticity aligned aggregates. Our work shows that the emergence of these structures at different shear rates is coincident with a peak in the viscosity and can be rescaled to a critical accumulated strain, which is a sensitive function of volume fraction.
|
Highly anisotropic vorticity aligned flocs of carbon black particles. Click to play movie [Flash] |
 |
| Fumed Alumina displays analogous behavior. movie [Flash] |
![]()
1.

