[next] [prev] [prev-tail] [tail] [up]

5 Chain Statistics: End-End Distances

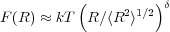
We can now return to the question of real chain statistics. Before, we derived the Gaussian distribution for idea chains and used it to arrive at an expression for the free energy of an ideal polymer chain as a function of its end-end distance. Now, for real polymer chains, we have a free energy that is a function of the scaling exponent ν (R ≈ bNν) where

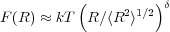
( )δ F(R) ≈ kT R∕⟨R2⟩1∕2

with δ = 1∕(1 - ν).

The probability distribution function for end-end distances is given by the Boltzmann factor using the free energy F(R)

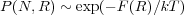
P(N, R) ~ exp(- F(R)∕kT)

This probability is further modified by the decreased likelihood of finding chain ends within a certain distance of each other that scales as Rg. If we define

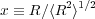
21∕2 x ≡ R∕⟨R ⟩

then

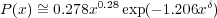P(x) ~= 0.278x0.28exp(- 1.206xδ)
(8)

For real chains, δ~ =2.43. The distribution of end-end distances is markedly lower at small distances than ideal chains.

[next] [prev] [prev-tail] [front] [up]