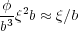
A favorable energetic interaction with a surface will lead to confinement of the chain to lie within a distance ξ of the surface, which defines the blob length scale. We can make a very simple analysis which neglects entropic considerations, and describe the blob scale as that beyond which the interaction energy is larger than thermal energy. We require an expression for the number of monomer segments in each blob that are in contact with the surface. If we make a mean field assumption for the density of monomer segments in the blob, then the number of contacts is just this number density multiplied by the volume that exists within b of the surface, i.e. bξ2.
The volume fraction of segments in the blob is given by φ ≈ (b3g∕ξ3) ≈ b∕ξ since ξ ≈ gb1∕2. The number density of monomers in the blob is φ∕b3 and so the number of monomers in contact with the surface is
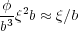
If the interaction energy with the surface is -δkT per monomer, then the energy gain per blob is simply
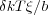
which is approximately kT at the length scale ξ. This provides the size of the blob
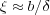
Since each adsorption blob is of a size that it contributes kT to the energy, the chain energy is
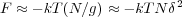 | (12) |