Generate ensembles of at least 1000 trajectories for an ideal random walk and a self-avoiding random walk (monomers cannot revisit an occupied point in space) on a cubic lattice. Make calculations for N=100, 500, 1000, 5000 and 10000 monomers or steps. The chain is allowed to take steps of unit length in any of the x, y or z directions.
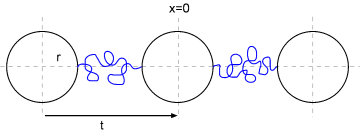
- Provide a plot and show how < R2 > scales with N in each case. Recall that
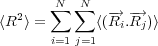
- What is the probability distribution function P(R) for N=10000?
- Calculate the radius of gyration, < Rg2 > and show how it varies with N. How does < R2 > ∕ < Rg2 > vary with
N? Recall that
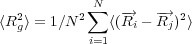
- Subdivide your ideal random walk N = 10000 chain by considering only every nth monomer where n = 2,4,8,32 and 128. Are the reduced trajectories still Gaussian in their statistics? At what n do they deviate?
Consider the pairwise interaction between uncharged colloidal particles, mediated by a polymer chain attached at their surfaces along a line joining their centers. We examine a linear arrangement of three such particles, as shown in Figure 1.
The attractive interaction between spherical particles due to Van der Waals forces is written as
![[ ( )]
Φ (s) = - A ∕6--2R2---+ -----2R2----- + ln ---s2 +-4Rs--
s2 + 4Rs s2 + 4Rs + 4R2 s2 + 4Rs + 4R2](HW1_w2x.png)
where s is the separation between the surfaces of the spheres (t - 2r in Figure 1), R is the radius of the spheres and A is the Hamaker constant. A good value for the Hamaker constant is 5E - 20 J or about 10 kT at room temperature. For R ≫ s, this expression reduces to
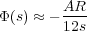
- Make a plot of the inter-particle potential (in units of kT) between the middle and either end particle due solely to the Van der Waals interaction, out to a center-center distance of 10r.
- Consider the displacement of the center particle away from equilibrium (x = 0). The free energy change associated
with the change in the end-end dimensions of the left and right polymers modifies the interaction potential between
the particles. Let’s examine polymers with Rg = r,r∕2 and r∕100, separated by t = 4r,8r and 16r (9 cases).
- Construct and plot the modified potentials (i.e. add the contribution from the polymer chains to the potential
from part I above) under the assumption that the chains are Gaussian. That is, they follow force-displacement
relationships of the form
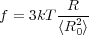
where < R0 > is the unperturbed end-end distance of the chain.
- Construct and plot the modified potentials under the assumption that the chains are worm-like. That is, they
follow force-displacement relationships of the form
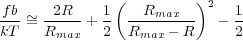
given Rmax = 50b. In the WLC model, b = 2lp and the radius of gyration is given by
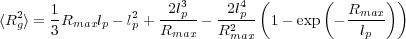
- Construct and plot the modified potentials (i.e. add the contribution from the polymer chains to the potential
from part I above) under the assumption that the chains are Gaussian. That is, they follow force-displacement
relationships of the form
- What other factors could be considered in this picture to make it more realistic?
Consider a polymer containing N Kuhn monomers (of length b) in a dilute solution where ideal chain statistics apply. The molar mass of the polymer is M.
- What is the mean-square end-to-end distance R02 of the polymer?
- What is the fully extended length Rmax?
- What is the mean-square radius of gyration Rg2 of this polymer?
- Estimate the overlap concentration c* for this polymer, assuming that the pervaded volume of the chain is a sphere of radius Rg
- How does this overlap concentration depend on the degree of polymerization
- What is the ratio of its fully extended length to the average root mean square end-to-end distance Rmax∕R0?
- Consider an example of a polymer with molar mass M = 104 g/mol. consisting of N = 100 Kuhn monomers (of length b = 10Å and determine R0, Rg, Rmax, c* and Rmax∕R0.
The concept of the tension blob was introduced to make a simple scaling argument for the force-extension response of a Gaussian chain. Describe the concept and its utility in your own words.